介绍

Fenwick树主要是用来解决数组前缀和的问题，其主要思想是在每个节点存储部分和和通过从叶节点到根节点遍历得到总和，树的高度为log(n)，主要有两个操作：Query和Update，时间复杂度均为log(n)

原理

Update

对某一节点的值进行修改，对应的sum值也会改变，同时依次更改到根节点所经过的所有节点值。

Query

在query的时候，树是另外一种的形态。需要计算从该节点到根节点所有值的和，即为前i的和sum[i]

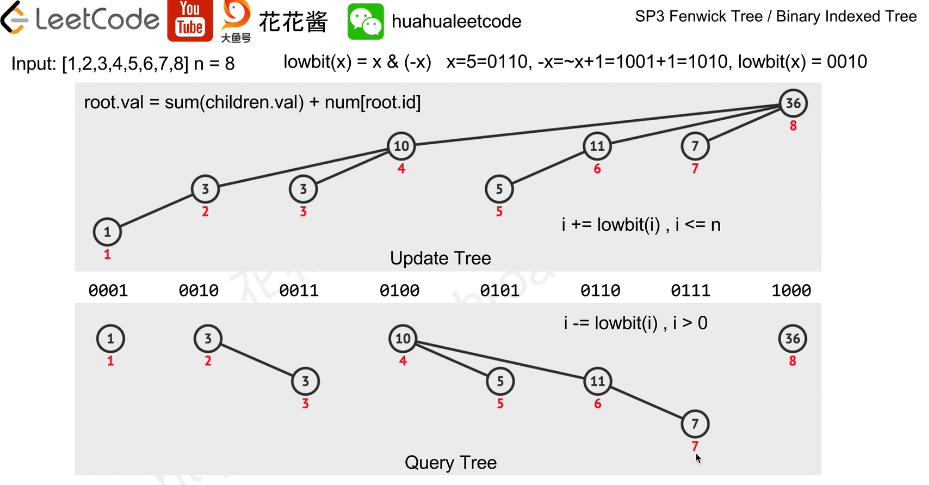
FinwickTree

实现

class FenwickTree {
public:
  FenwickTree(int n) : sums_(n+1, 0) {}
 
  void update(int i, int delta) {
    while (i < sums_.size()) {
      sums_[i] += delta;
      i += lowbit(i);
    }
  }
  
  int query(int i) const {
    int sum = 0;
    while (i > 0) {
      sum += sums_[i];
      i -= lowbit(i);
    }
    return sum;
  }
  
private:
  static inline int lowbit(int x) { return x&(-x); }
  vector<int> sums_;
};

应用

  1. LeetCode 493.翻转对

    给定一个数组nums，如果i < j且nums[i] > 2*nums[j]， 我们将(i, j)称为一个重要的翻转对。返回给定数组的重要翻转对的数量。

    示例1：

    输入： [1, 3, 2, 3, 1]

    输出： 2

    思路：

    主要是计算对于每一个2*num[j]，统计有多少个之前出现过的num[i]大于它。首先统计所有的nums[i]和2*nums[i]，并且去重处理。由于数据的范围较大，需要利用哈希表进行离散化处理，映射到连续的整数区间。最后也是最重要的是，利用树状数组来计算统计，并且更新数组。

class Solution {
public:
  int reversePairs(vector<int>& nums) {
    set<long long> allNumbers;
    for (int x : nums) {
      allNumbers.insert(x);
      allNumbers.insert((long long)x * 2);
    }
    // 利用哈希表进行离散化
    unordered_map<long long, int> values;
    int idx = 0;
    for (long long x : allNumbers) {
      values[x] = ++idx;
    }

    int ret = 0;
    FenwickTree bit(values.size());
    for (int i = 0; i < nums.size(); i++) {
      int left = values[(long long)nums[i] * 2], right = values.size();
      ret += bit.query(right) - bit.query(left);
      bit.update(values[nums[i]], 1);
    }
    return ret;
  }
};